[Algorithm][Python] 퀵 정렬 (quick sort)

1. 퀵 정렬 (quick sort) 이란?

• 정렬 알고리즘의 꽃
• 왜 꽃이냐> 왜 이게 정렬에 좋은것일까?
• 기준점 (pivot) 을 정해서, 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right) 으로 모으는 함수를 작성
• 각 왼쪽, 오른쪽은 재귀용법을 사용해서 다시 동일 함수를 호출하여 위 작업을 반복함
• 함수는 왼쪽 + 기준점 + 오른쪽을 리턴함

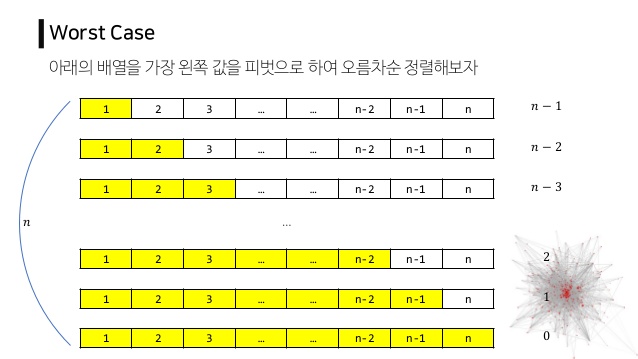
왜 퀵정렬이 꽃일까…? 거품 정렬 방식이 느린 이유는 필요없는 비교를 자주 수행하기 때문! 예를 들어서 a~1~,a~2~,a~3~ 와 같은 데이터가 있을 때 우리가 이미 a~1~ < a~2~ 이고 a~2~ < a~3~ 이라는 사실을 알았다면, 굳이 a~1~ 과 a~3~을 비교하지 않고도 a~1~ < a~3~ 임을 알 수 있기 때문이다. 퀵정렬의 경우? 왼쪽과 오른쪽으로 나누는데, 왼쪽과 오른쪽은 더이상 비교할 필요가 없다. pivot 에 의해 값차이가 난다는 것을 알기 때문!!!

2. 어떻게 코드로 만들까?

• 리스트를 리스트 슬라이싱 (예: [:2]) 을 이용해서 세개로 짤라서 각 리스트 변수에 넣고 출력하기
• 리스트를 맨 앞에 데이터를 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
• 맨 앞 데이터를 pivot 변수에 넣고, pivot 기준 작은데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
• data_list 가 임의 길이일 때, 맨 앞 데이터를 기준(pivot) 으로 작은데이터는 left, 큰 데이터는 right 에 넣기

import random
data_list = random.sample(range(100), 10)

left = list()
right = list()
pivot = data_list[0]

for index in range(1, ----):
	if data_list[index] < pivot:
		left.append(data_list[index])
	else:
		right.append(data_list[index])

3. 알고리즘 구현

• quicksort 함수 만들기
  • 만약 리스트 갯수가 한개이면 해당 리스트 리턴
  • 그렇지 않으면 리스트 맨 앞의 데이터를 기준점으로 놓기
  • left right 변수를 만들고
  • 맨 앞의 데이터를 뺀 나머지 데이터를 기준점과 비교
    • 작으면 left.append
    • 크면 right.append
  • return quick_sort(left) + [pivot] + quick_sort(right) 로 재귀호출!

def quick_sort(data):
	if len(data) <= 1:
		return data
	left = list()
	right = list()
	pivot = data[0]
	for index in range(1, len(data)):
		if pivot > data[index]:
			left.append(data[index])
		else:
			right.append(data[index])
	return quick_sort(left) + [pivot] + quick_sort(right)

프로그래밍 연습
위 퀵정렬 코드를 파이썬 list comprehension을 사용해서 더 깔끔하게 작성해보기

def qsort(data):
	if len(data) <=1 :
		return data
	pivot = data[0]
	left = [item for item in data[1:] if item < pivot]
	right = [item for item in data[1:] if item > pivot]

	return qsort(left) + [pivot] + qsort(right)

4. 알고리즘 특징

• 병합정렬과 유사, 시간복잡도는 O(n log n)
  • 단, 최악의 경우 - 맨 처음 pivot이 가장 크거나, 가장 작으면 - 모든 데이터를 비교하는 상황이 나옴 - O($n^2$)

출처

https://modoocode.com/248