해쉬 테이블 (Hash Table)

1. 해쉬 구조

Hash Table: 키(key)에 데이터(Value)를 저장하는 데이터 구조
- Key를 통해 바로 데이터를 받아올 수 있으므로, 속도가 획기적으로 빨라짐
- 파이썬 딕셔너리(Dictionary)타입이 해쉬테이블의 예: Key를 가지고 바로 데이터(Value)를 꺼냄
- 보통 배열로 미리 Hash Table 사이즈만큼 생성 후에 사용 (공간과 탐색시간을 맞바꾸는 기법)
- 단, 파이썬에서는 해쉬를 별도 구현할 이유가 없음 - 딕셔너리 타입을 사용하면 됨

2. 알아둘 용어

해쉬(Hash): 임의 값을 고정 길이로 변환하는 것
해쉬 테이블(Hash Table): 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
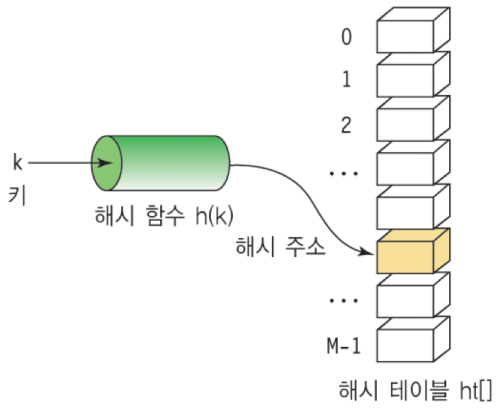
해싱 함수(Hashing Function) : Key에 대해 산술 연산을 이용해 데이터 위치를 찾을 수 있는 함수
해쉬 값(Hash Value) 또는 해쉬 주소(Hash Address) : Key 를 해싱 함수로 연산해서, 해쉬 값을 알아내고, 이를 기반으로 해쉬 테이블에서 해당 Key에 대한 데이터 위치를 일관성 있게 찾을 수 있음
슬롯(Slot) : 한 개의 데이터를 저장할 수 있는 공간
저장할 데이터에 대해 Key를 추출할 수있는 별도 함수도 존재할 수 있음.

출처: https://www.fun-coding.org/00_Images/hash.png

3. 간단한 해쉬 예

3.1. hash table 만들기

참고 : 파이썬 list comprehension - https://www.fun-coding.org/PL&OOP5-2.html

  
[출력표현식 for 요소 in 입력Sequence [if 조건식]]

입력 Sequence 는 Iteration이 가능한 데이타 Sequence 혹은 컬렉션
[if 조건식] 에서 [] 은 리스트 괄호가 아니라, 옵션이라는 뜻. 조건이 있을때만 넣으면 된다는 뜻.

  
# 예: 종류가 다른 데이터에서 정수 리스트만 가져오기
dataset = [4, True, 'Dave', 2.1, 3]

int_data = [num for num in dataset if type(num) == int]

int_data # [4,3]

print(type(int_data)) # <class 'list'>

  
#출력 표현식을 num * num 으로 바꿔볼까요?
int_square_data = [num * num for num in dataset if type(num) == int]

int_square_data # [16, 9]

  
hash_table = list([i for i in range(10)])
hash_table

# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

3.2. 이번에는 초간단 해쉬 함수를 만들어보자.

다양한 해쉬 함수 고안 기법이 있으며, 가장 간단한 방식이 Division법 (나누기를 통한 나머지 값을 사용하는 기법)

  
def hash_func(key):
	return key % 5

3.3. 해쉬 테이블에 저장해보자.

데이터에 따라 필요시 key 생성 방법 정의가 필요

  
data1 = 'Andy'
data2 = 'Dave'
data3 = 'Trump'
data4 = 'Anthor'

## ord(): 문자의 ASCII(아스키)코드를 리턴한다. 아스키코드란? 영어랑 특수문자를 코드로 표현하는 것. 최근에는 Uni-Code 로 표현한다.
print (ord(data1[0]), ord(data2[0]), ord(data3[0]))
print (ord(data1[0]), hash_func(ord(data1[0])))
print (ord(data1[0]), ord(data4[0]))

# 65  68  84
# 65  0
# 65  65

3.3.2. 해쉬 테이블에 값 저장 예
- data: value 와 같이 data 와 value 를 넣으면, 해당 data 에 대한 key 를 찾아서 해당 key 에 대응하는 해쉬 주소에 value 를 저장하는 예
  1 2 3 4 def storage_data(data, value): key = ord(data[0]) hash_address = hash_func(key) has_table[hash_address] = value

3.4. 해쉬 테이블에서 특정 주소의 데이터를 가져오는 함수도 만들어보자.

  
storage_data('Andy', '01055553333')
storage_data('Dave', '01044443333')
storage_data('Trump', '01022223333')

3.5. 실제 데이터를 저장하고 읽어보자.

  
def get_data(data):
	key = ord(data[0])
	hash_address = hash_func(key)
	return hash_table[hash_address]

get_data('Andy')

# '01055553333'

4. 자료 구조 해쉬 테이블의 장단점과 주요 용도

장점
- 데이터 저장/읽기 속도가 빠르다. (검색 속도가 빠르다.)
- 해쉬는 키에 대한 데이터가 있는지(중복) 확인이 쉬움
단점
- 일반적으로 저장공간이 좀더 많이 필요하다.
- 여러 키에 해당하는 주소가 동일할 경우 충돌을 해결하기 위한 별도 자료구조가 필요함
주요 용도
- 검색이 많이 필요한 경우
- 저장, 삭제, 읽기가 빈번한 경우
- 캐쉬 구현시 (중복 확인이 쉽기 때문)

5. 프로그래밍 연습

연습1: 리스트 변수를 활용해서 해쉬 테이블 구현해보기
1. 해쉬 함수: key % 8
2. 해쉬 키 생성: hash(data) = (파이썬 내장 메소드) 애초에 파이썬은 해시함수를 제공함

hash() 함수는 파이썬 내장함수다. 요즘에는 잘 안쓰는데, 그 이유가 해시값이 매번 바뀌기 때문이다.

  
hash_table = list([0 for i in range(8)])

def get_key(data):
	return hash(data) # 파이썬 내장 메소드

def hash_function(key):
	return key % 8

def save_data(data, value):
	hash_address = hash_function(get_key(data))
	hash_table[hash_address] = value

def read_data(data):
	hash_address = hash_function(get_key(data))
	return hash_table[hash_address]

  
save_data('Dave', '0102030200')
save_data('Andy', '01033232200')
read_data('Dave')

#'0102030200'

hash_table
# [ '0102030200', 0, 0, 0, 0, 0, 0, '01033232200' ]

6. 충돌( Collision ) 해결 알고리즘 (좋은 해쉬 함수 사용하기)

해쉬 테이블의 가장 큰 문제는 충돌(Collision)의 경우다. 이 문제를 충돌 또는 해쉬 충돌 이라고 부른다.

6.1. Chaining 기법

개방 해슁 또는 Open Hashing 기법 중 하나: 해쉬 테이블 저장공간 외의 공간을 활용하는 기법
충돌이 일어나면, 링크드 리스트라는 자료 구조를 사용해서, 링크드 리스트로 데이터를 추가로 뒤에 연결시켜서 저장하는 기법

연습2: 연습1의 해쉬 테이블 코드에 Chaining 기법으로 충돌해결 코드를 추가해보기
1. 해쉬 함수: key % 8
2. 해쉬 키 생성: hash(data)

  
hash_table = list([0 for i in range(8)])
# [0, 0, 0, 0, 0, 0, 0, 0]

def get_key(data):
	return hash(data)

def hash_function(key):
	return key % 8

def save_data(data, value):
	index_key = get_key(data)
	hash_address = hash_function(index_key)
	if hash_table[hash_address] !== 0: # 해시테이블에서 해당 address의 값이 0 이 아닌경우, 즉 이미 값이 존재하는 경우
		for index in range(len(hash_table[hash_address])): # 해당 address 에 해당하는 배열을 순회한다.
			if hash_table[hash_address][index][0] == index_key: # 배열에서 index 번째 요소의 0번째 요소가 index_key와 같다면
				hash_table[hash_address][index][1] = value # 첫번째 요소를 value 로 해줌, 즉 바뀌는 것이 없음. 왜 이렇게 했을까?
				return
		hash_table[hash_address].append([index_key, value]) # 해당하는 값이 없다면, 새로운 배열(키값과 value)를 append 시켜줌
	else:
		hash_table[hash_address] = [[index_key, value]] # 만약 해시테이블에서 hash_table[hash_address] == 0 이면 그냥 값을 할당해줌

  
print(hash('Dave') % 8)
print(hash('Dd') % 8)
print(hash('Data') % 8)

# 5 5 6

  
save_data('Dave', '1201023010')
save_data('Data', '3301023010')
save_data('Dave', '01034340992')

print(hash_table)

[0,
 0,
 0,
 0,
 0,
 [[2517405733183364333, '1201023010'], [-464815633440241563, '01034340992']],
 [[4167812268688963486, '3301023010']],
 0]

6.2. Linear Probing 기법

체이닝 기법에 반대 개념
폐쇄해싱, 또는 Close Hashing 기법 중 하나: 해쉬 테이블 저장공간 ‘안’에서 충돌문제를 해결하는 기법
충돌이 일어나면, 해당 hash address의 다음 address부터 맨 처음 나오는 빈공간에 저장하는 기법
- 저장공간 활용도를 높이기 위한 기법

연습3: 연습1의 해쉬 테이블 코드에 Linear Probling 기법으로 충돌해결 코드를 추가해보기
1. 해쉬 함수: key % 8
2. 해쉬 키 생성: hash(data)

  
hash_table = list([0 for i in range(8)])

def get_key(data):
	return hash(data)

def hash_function(key):
	return key % 8

def save_data(data, value):
	index_key = get_key(data)
	hash_address = hash_function(index_key)
	if hash_table[hash_address] != 0: # 해시테이블에서 입력된 data에 해당하는 해시테이블에 데이터가 있는경우? 즉 충돌이 일어난 경우다.
		for index in range(hash_address, len(hash_table)): # hash_address 부터 hash_table. 길이까지 순회한다.
		# Linear Probing = Close Hashing 의 경우, 충돌이 일어나면 해당 hash address 의 다음 address 부터
		# 처음 나오는 빈공간에 저장하는거기 때문.
			if hash_table[index] == 0: # 순회 요소가 0인경우: 즉 데이터가 없는 경우는 바로 삽입
				hash_table[index] = [index_key, value]
				return
			elif hash_table[index][0] == index_key: # 데이터가 있고, 0번째 요소가 같으면 업데이트 해주기
				hash_table[index][1] = value
				return

	 else:
		 hash_table[hash_address] = [index_key, value] # 빈공간이면 데이터 바로 삽입

def read_data(data):
	index_key = get_key(data)
	hash_address = hash_function(index_key)

	if hash_table[hash_address] != 0:
		for index in range(hash address, len(hash_table)):
			if hash_table[index] == 0:
				return None
			elif hash_table[index][0] == index_key:
				return hash_table[index][1]
	else:
		return None

read_data를 왜 이런식으로 작성했는지 모르겠다. 그냥 data 를 가지고 hash_address 검색 후, 값이 있으면 표기하고 아니면 None 을 리턴하면 되는것 아닌가?
위에 식에서는 한번 순회하고, 값이 없으면 none을 리턴한다고 중복으로 써놓았다.

  
print( hash('dk') % 8)
print( hash('da') % 8)
print( hash('dc') % 8)

# 7 2 4

  
save_data('dk', '01200123123')
save_data('da', '333333333')
save_data('dc', '01034340992')

print(hash_table)

  
[0, 0, [-8247022340911430670, '3333333333'], 0, [8923840923840239,'01034340992'], 0, 0, [4625843833139520663, '01200123123']]

6.3. 빈번한 충돌을 개선하는 기법

해쉬 함수를 재정의 및 해쉬 테이블 저장공간을 확대
예:

  
has_table = list([None for I in range(16)])

def hash_function(key):
	return key % 16

# 기존 8개 에서 16개로 저장공간을 확대

참고 : 해쉬 함수와 키 생성함수

파이썬의 hash() 함수는 실행할 때마다, 값이 달라질 수 있음
유명한 해쉬 함수들이 있음: SHA( Secure Hash Algorithm, 안전한 해시 알고리즘)
- 어떤 데이터도 유일한 고정된 크기의 고정값을 리턴해주므로, 해쉬 함수로 유용하게 활용가능

SHA-1

  
import hashlib

data = 'test'.encode()
hash_obect = hashlib.sha1()
hash_object.update(data)
hex_dig = hash_object.hexdigest()
print (hex_dig)

# a94a8fe5ccb19ba61c4c0873d391e987982fbbd3

SHA-256

  
import hashlib

data = 'test'.encode()
hash_object = hashlib.sha256()
hash_object.update(data)
hex_dig = hash_object.hexdigest()
print (hex_dig)

# 9f86d081884c7d659a2feaa0c55ad015a3bf4f1b2b0b822cd15d6c15b0f00a08

7. 시간 복잡도

일반적인 경우(Collision 이 없는 경우) 는 O(1)
최악의 경우 (Collision 이 모두 발생하는경우, 즉 충돌해시) 는 O(n)
해쉬 테이블의 경우, 일반적인 경우를 기대하고 만들기 때문에 , 시간복잡도는 사실 O(1) 이라고 말할 수 있음.

검색에서 해쉬 테이블의 사용 예

16개의 배열에 데이터를 저장하고 검색할 때 O(n)
16개의 데이터 저장공간을 가진 위의 해쉬 테이블에 데이터를 저장하고 검색할 때 O(1)

[Algorithm][Python] 해시 테이블(hash table)